11.3.2 Shadow Volumes

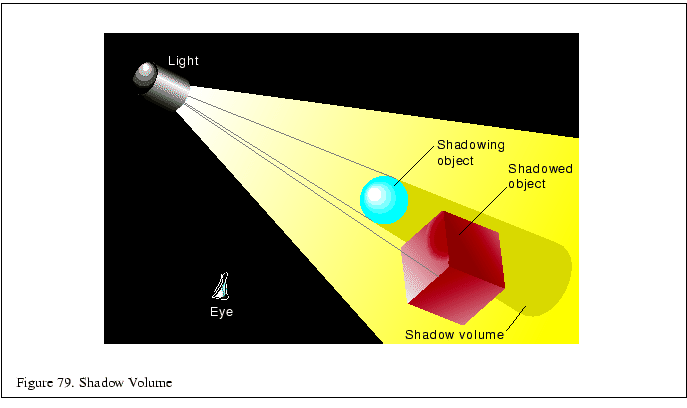
This technique treats the shadows cast by objects as polygonal volumes. The stencil buffer is used to find the intersection between the polygons in the scene and the shadow volume [21,8,52].

The shadow volume is constructed from rays cast from the light source, intersecting the vertices of the shadowing object, then continuing outside the scene. Defined in this way, the shadow volumes are semi-infinite pyramids, but the same results can be obtained by truncating the base of the shadow volume beyond any object that might be shadowed by it. This gives you a polygonal surface, whose interior volume contains shadowed objects or parts of shadowed objects. The polygons of the shadow volume are defined so that their front faces point out from the shadow volume itself.

The stencil buffer is used to compute which parts of the objects in the scene are in the shadow volume. It uses a non-zero winding rule technique. For every pixel in the scene, the stencil value is incremented as it crosses a shadow boundary going into the shadow volume, and decrements as it crosses a boundary going out. The stencil operations are set so this increment and decrement only happens when the depth test passes. As a result, pixels in the scene with non-zero stencil values identify the parts of an object in shadow.

Since the shadow volume shape is determined by the vertices of the shadowing object, it's possible to construct a complex shadow volume shape. Since the stencil operations will not wrap past zero, it's important to structure the algorithm so that the stencil values are never decremented past zero, or information will be lost. This problem can be avoided by rendering all the polygons that will increment the stencil count first (i.e., the front facing ones), then rendering the back facing ones.

Another issue with counting is the position of the eye with respect to the shadow volume. If the eye is inside a shadow volume, the count of objects outside the shadow volume will be $-1$, not zero. This problem is discussed in more detail in Section 11.3. The algorithm takes this case into account by initializing the stencil buffer to 1 if the eye is inside the shadow volume.

Here's the algorithm for a single shadow and light source:

1. The color buffer and depth buffer are enabled for writing, and depth testing is enabled.
2. Set attributes for drawing in shadow. Turn off the light source.
3. Render the entire scene.
4. Compute the polygons enclosing the shadow volume.
5. Disable the color and depth buffer for writing, but leave the depth test enabled.
6. Clear the stencil buffer to 0 if the eye is outside the shadow volume, or 1 if inside.
7. Set the stencil function to always pass.
8. Set the stencil operations to increment if the depth test passes.
9. Turn on back face culling.
10. Render the shadow volume polygons.
11. Set the stencil operations to decrement if the depth test passes.
12. Turn on front face culling.
13. Render the shadow volume polygons.
14. Set the stencil function to test for equality to 0.
15. Set the stencil operations to do nothing.
16. Turn on the light source.
17. Render the entire scene.

When the entire scene is rendered the second time, only pixels that have a stencil value equal to zero are updated. Since the stencil values were only changed when the depth test passes, this value represents how many times the pixel's projection passed into the shadow volume minus the number of times it passed out of the shadow volume before striking the closest object in the scene (after that the depth test will fail). If the shadow boundary was crossed an even number of times, the pixel projection hit an object that was outside the shadow volume. The pixels outside the shadow volume can therefore ``see'' the light, which is why it is turned on for the second rendering pass.

For a complicated shadowing object, it make sense to find its silhouette vertices, and use only these for calculating the shadow volume. These vertices can be found by looking for any polygon edges that either (1) surround a shadowing object composed of a single polygon, or (2) is shared by two polygons, one which is facing towards the light source, one which is facing away. You can determine which direction the polygons are facing by taking a dot product of the polygon's facet normal with the direction of the light source, or by a combination of selection and front/back face culling