


Next: 13.3.3 Convolutions Using the
Up: 13.3.2 The Convolution Operation
Previous: 13.3.2.1 Two-Dimensional Convolutions
Contents
In the general case, the two-dimensional convolution operation
requires
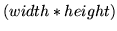 multiplications for each output pixel.
Separable filters are a special case of general convolution in which
the filter
multiplications for each output pixel.
Separable filters are a special case of general convolution in which
the filter
can be expressed in terms of two vectors
such that for each
![$(i,j) \epsilon ([0..(width-1)], [0..(height-1)])$](img384.gif)
If the filter is separable, the convolution operation may be performed
using only
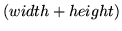 multiplications for each output pixel.
Applying the separable filter to Equation15 becomes:
multiplications for each output pixel.
Applying the separable filter to Equation15 becomes:
Which can be simplified to:
To apply the separable convolution, first apply 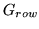 as though
it were a
as though
it were a 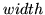 by
by 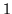 filter. Then apply
filter. Then apply 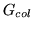 as though it
were a
as though it
were a 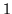 by
by 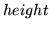 filter.
filter.
2001-01-10
![]() multiplications for each output pixel.
Separable filters are a special case of general convolution in which
the filter
multiplications for each output pixel.
Separable filters are a special case of general convolution in which
the filter
![\begin{displaymath}
H[x][y] = \sum^{height - 1}_{j = 0}\sum^{width - 1}_{i = 0}
F[x+i][y+j]G_{row}[i]G_{col}[j]
\end{displaymath}](img387.gif)
![\begin{displaymath}
H[x][y] = \sum^{height - 1}_{j = 0}G_{col}[j]\sum^{width - 1}_{i = 0}F[x+i][y+j]G_{row}[i]
\end{displaymath}](img388.gif)