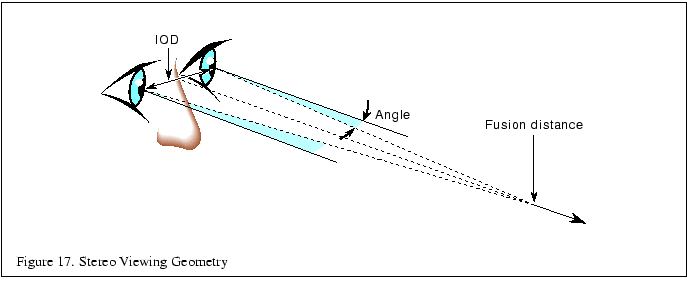
The other parameter is the distance from the eyes where the lines of sight for each eye converge. This distance is called the fusion distance. At this distance objects in the scene will appear to be on the front surface of the display (``in the glass''). Objects farther than the fusion distance from the viewer will appear to be ``behind the glass'' while objects in front will appear to float in front of the display. The latter illusion is harder to maintain, since real objects visible to the viewer beyond the edge of the display tend to destroy the illusion.
Although it is possible to create good looking stereo scenes using dimensionless quantities, the best behavior occurs when everything is measured carefully. This is easy to do if the glFrustum() call is used rather than the gluPerspective() call. Pick a unit of measurement, then use those units for screen size, distance from viewer to screen, interocular distance, and so forth. It is a good idea to keep the code that computes the screen parameters separate from the rest of the application, to make it easier to port the program to different screen sizes or arrangements.
The view direction vector and the vector separating the left and right eye position are perpendicular to each other. The two view points are located along a line perpendicular to the direction of view and the ``up'' direction. The fusion distance is measured along the view direction. The position of the viewer can be defined to be at one of the eye points, or halfway between them. In either case, the left and right eye locations are positioned relative to it.
If the viewer is taken to be halfway between the stereo eye positions,
and assuming gluLookAt() has been called to put the viewer position
at the origin in eye space, then the fusion distance is measured along
the negative 
axis (like the near and far clipping planes),
and the two viewpoints are on either side of the origin along the 
axis,
at (-IOD/2, 0, 0) and (IOD/2, 0, 0).
