17.8 Other Atmospheric Effects

OpenGL provides a primitive capability for rendering atmospheric effects such as fog, mist and haze. It is useful to simulate the affects of atmospheric effects on visibility to increase realism, and it allows the database designer to cover up a multitude of sins such as ``dropping'' polygons near the far clipping plane in order to sustain a fixed frame rate.

OpenGL implements fogging by blending the fog color with the incoming fragments using a fog blending factor, $f$,

$$C = f C_{in} + (1-f) C_{fog}$$

This blending factor is computed using one of three equations: exponential (GL_ EXP), exponential-squared (GL_ EXP2), and linear (GL_ LINEAR)

$$\begin{eqnarray*} f & = & e^{-(density \cdot z)} \\ f & = & e^{{-(density \cdot z)}^2} \\ f & = & { end - z } \over {end - start} \end{eqnarray*}$$

where $z$ is the eye-coordinate distance between the viewpoint and the fragment center.

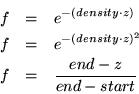
Linear fog is frequently used to implement intensity depth-cuing in which objects closer to the viewer are drawn at higher intensity [30]. The effect of intensity as a function of distance is achieved by blending the incoming fragments with a black fog color.

The exponential fog equation has some physical basis. It is the result of integrating a uniform attenuation between the object and the viewer. The exponential-squared function includes the attenuation for reflected light which has passed through the attenuation layer twice, once for the incident path and again for the reflected path. The exponential and exponential-squared functions can be used to represent a number of atmospheric effects using different combinations of fog colors and density values. Since OpenGL does not fog the pixel values during a clear operation, the value of $f$ at the far plane, $far$,

$$f_{far} = e^{-(density \cdot far)}$$

can be used to determine the color to which to clear the background

$$C_{bg} = f_{far} C_{in} + (1-f_{far}) C_{fog}$$

where $C_{in}$ is the color to which the background would be cleared without fog enabled.

As mentioned earlier, the obscured visibility of objects near the far plane can be exploited to overcome various problems such as drawing time overruns, level-of-detail transitions, and database paging. However, in practice it has been found that the exponential function does not attenuate distant fragments rapidly enough, so exponential-squared fog can be used to achieve a sharper fall-off in visibility. Some vendors have gone a step further and provided more control over the fog function by allowing applications to control the fog value through a spline curve.

There are other problems that OpenGL's primitive fog model does not address. For example, emissive geometry such as the light points described above should be attenuated less severely than non-emissive geometry. This effect can be approximated by precompensating the color values for emissive geometry, or reducing the fog density when emissive geometry is drawn. Neither of these solutions is completely satisfactory since colors values are clamped to 1.0 in OpenGL, limiting the amount of precompensation that can be done. Many OpenGL implementations use lookup table methods to efficiently compute the fog function, so changes to the fog density may result in expensive table recomputations. To overcome this problem some vendors have provided a mechanism to bias the eye-coordinate distance, avoiding the need to recompute the fog lookup table.

If OpenGL fog processing is bypassed it is possible to do more sophisticated atmospheric effects using multipass techniques. The OpenGL fog computation can be thought of as simple table lookup using the eye-coordinate distance. The result is used as a blend factor for blending between the fragment color and fog color. A similar operation can be implemented using glTexGen() to generate the eye-coordinate distance for each fragment and a 1D texture for the fog function. Using a specially constructed 2D or 3D texture and a more sophisticated, texture coordinate generation function, it is possible to compute more complex fog functions incorporating parameters such as altitude and eye-coordinate distance.