Bump mapping [9], like texture mapping, is a technique to add more realism to synthetic images without adding a lot of geometry. Texture mapping adds realism by attaching images to geometric surfaces. Bump mapping adds per-pixel surface relief shading, increasing the apparent complexity of the surface by perturbing the surface normal. Surfaces that have a patterned roughness are good candidates for bump mapping. Examples include oranges, strawberries, stucco, wood, etc.
An intuitive representation of surface bumpiness is formed by a 2D height field array, or bump map. This bump map is defined by the scalar difference F(u,v) between the flat surface P(u,v) and the desired bumpy surface P'(u,v) along the normal N at each point u,v. Typically the function P is modeled separately as polygons or parametric patches and F is modeled as a 2D image using a painting program or other image processing tool.
Rather than subdivide the surface P'(u,v) into regions that are locally flat, observe that the shading perturbations on such a surface depend more on perturbations in the surface normal than on the position of the surface itself. A technique perturbing only the surface normal at shading time achieves similar results without the processing burden of subdividing geometry. (Note that this technique does not perturb shadows from other surfaces falling on the bumps or shadows from bumps on the same surface, so such shadows will retain their flat appearance.)
The normal vector ![]() at u,v can be calculated by the cross
product of the partial derivatives of P' in u and v. (The notational
simplification P'u is used here to mean the partial derivative
of P' with respect to u, sometimes written
at u,v can be calculated by the cross
product of the partial derivatives of P' in u and v. (The notational
simplification P'u is used here to mean the partial derivative
of P' with respect to u, sometimes written
![]() .)
The chain rule can be applied to the partial derivatives to yield the following expression of P'u P'v in terms of P, F, and derivatives
of F:
.)
The chain rule can be applied to the partial derivatives to yield the following expression of P'u P'v in terms of P, F, and derivatives
of F:
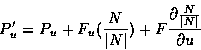
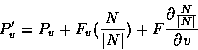
If F is assumed to be sufficiently small, the final terms of each of the previous expressions can be approximated by zero:
Expanding the cross product
![]() gives the following
expression for N':
gives the following
expression for N':
Which evaluates to:
Because
![]() yields the normal N and
yields the normal N and
![]() yields 0, we
can further simplify the expression for N' as follows:
yields 0, we
can further simplify the expression for N' as follows:
The values Fu and Fv are easily computed through forward differencing from the 2D bump map, and Pu and Pv can be computed either directly from the surface definition or from forward differencing applied to the surface parameterization.