Recall that the bump map normal ![]() is formed by
is formed by
![]() .
Assume that the surface P is coincident
with the XY plane and that changes in u and v correspond to changes
in X and Y, respectively. Then F can be substituted for P',
resulting in the following expression for the vector N':
.
Assume that the surface P is coincident
with the XY plane and that changes in u and v correspond to changes
in X and Y, respectively. Then F can be substituted for P',
resulting in the following expression for the vector N':
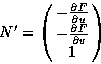
In order to evaluate the lighting equation, N' must be normalized.
If the displacements in the bump map are restricted to small values,
however, the length of N' will be so close to one as to be
approximated by one. Then N' itself can be substituted for
![]() without normalization. If the diffuse intensity component
without normalization. If the diffuse intensity component
![]() of the lighting equation is evaluated with the
value presented above for N', the result is the following:
of the lighting equation is evaluated with the
value presented above for N', the result is the following:
This expression requires the surface to lie in the XY plane and that
the u and v parameters change in X and Y, respectively. Most
surfaces, however, will have arbitrary locations and orientations in space.
In order to use this simplification to perform bump mapping, the
view direction ![]() ,
and
light source direction
,
and
light source direction ![]() are transformed into tangent space.
are transformed into tangent space.
Tangent space has 3 axes, ![]() ,
,
![]() and
and ![]() .
The tangent vector,
.
The tangent vector, ![]() ,
is parallel to the direction of
increasing s on the surface. The normal vector,
,
is parallel to the direction of
increasing s on the surface. The normal vector, ![]() ,
is perpendicular to the surface. The binormal,
,
is perpendicular to the surface. The binormal, ![]() ,
is perpendicular to both
,
is perpendicular to both ![]() and
and ![]() ,
and like
,
and like
![]() ,
lies in the plane tangent to the surface. These vectors
form a coordinate system that is attached to and varies over the surface.
,
lies in the plane tangent to the surface. These vectors
form a coordinate system that is attached to and varies over the surface.
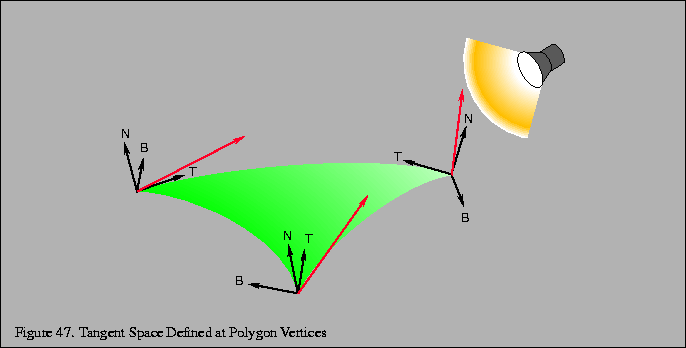
The light source is transformed into tangent space at each vertex of the
polygon. To find the tangent space vectors at a vertex, use the vertex
normal for ![]() and find the tangent axis
and find the tangent axis ![]() by finding
the vector direction of increasing s in the object's coordinate
system. The direction of increasing t may also be used.
Find
by finding
the vector direction of increasing s in the object's coordinate
system. The direction of increasing t may also be used.
Find ![]() by computing the cross product of
by computing the cross product of ![]() and
and
![]() .
These unit vectors form the transformation shown below:
.
These unit vectors form the transformation shown below:
This transformation brings coordinates into tangent space, where the plane tangent to the surface lies in the X-Y plane, and the normal to the surface coincides with the Z axis. Note that the tangent space transformation varies for vertices representing a curved surface, and so this technique makes the approximation that curved surfaces are flat and the tangent space transformation is interpolated from vertex to vertex.