10.6.0.4 Forward Differencing

The first derivative of the height values of the bump map in a given direction $s',t'$ can be approximated by the following process:

1. Render the bump map texture.
2. Shift the texture coordinates at the vertices by $s',t'$.
3. Re-render the bump map texture, subtracting from the first image.

Consider a one dimensional bump map for simplicity. The map only varies as a function of $s$. Assuming that the height values of the bump map can be represented as a height function $F(s)$, then the three step process above would be the following: $F(s) - F(s + \Delta s)$. If the delta is one texel in $s$, then the resulting texture coordinate is $F(s) - F(s + \frac{1}{w})$, where $w$ is the width of the texture in texels. This operation implements a forward difference of $F$, which would approximate the first derivative of $F$ if $F$ was continuous.

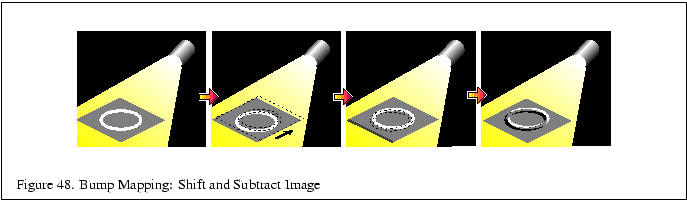
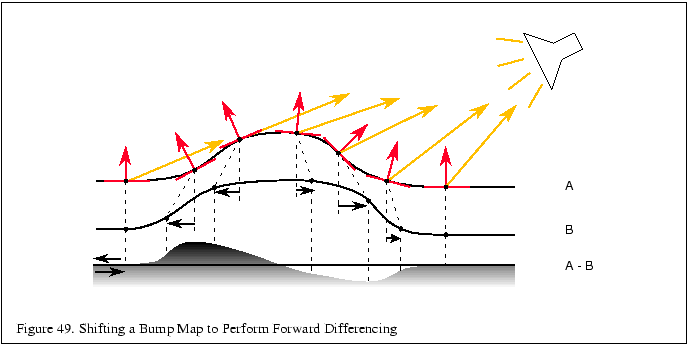
In the two dimensional case, the height function is $F(s,t)$, and performing the forward difference in the direction of $s',t'$ evaluates the derivative of $F(s,t)$ in the direction $s',t'$. This technique is also used to create embossed images.

This operation provides the values used for the first two addends shown in Equation 1. In order to provide the third addend of the dot product, the process needs to compute and add the transformed $z$ component of the light vector. The tangent space transform in Equation 2 implies that the transformed $z$ component of $L$ is simply the inner product of the vertex normal and the light vector, $N \cdot L$. Therefore, the $z$ component can be computed using OpenGL to evaluate the diffuse lighting term at each vertex. This computation is performed as a second pass, adding to the previous results.

The steps for diffuse bump mapping are the following:

1. Render the polygon with the bump map textured on it. Since the bump map modifies the polygon color, you can get the diffuse color you want by coloring the polygon with $k_d$. Lighting is disabled.
2. Find $\vec{N}$, $\vec{T}$ and $\vec{B}$ at each vertex.
3. Use the vectors to create a transformation.
4. Use the matrix to rotate the light vector $\vec{L}$ into tangent space.
5. Use the rotated $x$ and $y$ components of $\vec{L}$ to shift the $s$ and $t$ texture coordinates at each polygon vertex.
6. Re-render the bump map textured polygon using the shifted texture coordinates.
7. Subtract the second image from the first.
8. Render the polygon smooth shaded with lighting enabled and texturing disabled.
9. Add this image to result.

Using the accumulation buffer can improve the accuracy of this technique. The bump mapped objects in the scene are rendered with the bump map, re-rendered with the shifted bump map and accumulated with a negative weight, then re-rendered again using Gouraud shading and no bump map texture, accumulated normally.

The process can also be extended to find bump mapped specular highlights. The process is repeated using the halfway vector ($\vec{H}$) instead of the light vector. The halfway vector is computed by averaging the light and viewer vectors $\frac{\vec{L} + \vec{V}}{2}$. The combination of the forward difference of the bump map in the direction of the tangent space $\vec{H}$ and the $z$ component of $\vec{H}$ approximate $N \cdot H$. Here are the steps for computing $(\vec{N} \cdot \vec{H})$:

1. Render the polygon with the bump map textured on it.
2. Find $\vec{N}$, $\vec{T}$ and $\vec{B}$ at each vertex.
3. Use the vectors to create a rotation matrix.
4. Use the matrix to rotate the halfway vector $\vec{H}$ into tangent space.
5. Use the rotated $x$ and $y$ components of $\vec{H}$ to shift the $s$ and $t$ texture coordinates at each polygon vertex.
6. Re-render the bump map textured polygon using the shifted texture coordinates.
7. Subtract the second image from the first.
8. Render the polygon Gouraud shaded with no bump map texture, this time use $\vec{H}$ instead of $\vec{L}$. Use a polygon whose color is equal to the specular color you want, $k_s$.

The result must be raised to the shininess exponent before blending.

One technique for performing this exponential is to use the texture color table extension to perform a table lookup on the results of $(\vec{H} \cdot \vec{N})$. Invoke glColorTableSGI() with GL_ TEXTURE_COLOR_TABLE_SGI as its target, then enable GL_ TEXTURE_COLOR_TABLE_SGI. Copy the image calculated above from framebuffer memory into texture, using glCopyTexImage2D(). Finally, apply a projective texture transformation or calculate texture coordinates so that the specular component is mapped onto the object with the same screen coordinates in which it was drawn. Pixels copied from other objects drawn will not fall on the bump mapped object and will be discarded. It is a good idea to copy only the rectangular screen region that bounds the bump-mapped object if the application supports this. If the texture color table extension is not available, it may be possible to use glReadPixels(), glTexSubImage2D(), apply the exponent on the host, and still retain interactivity for small regions.

Another possibility is to use glCopyPixels() with a color table configured with glPixelMap(). The bump mapped object can be applied to the stencil buffer to create a mask so that only the pixels covered by the bump mapped object are applied to the framebuffer.

Finally, use blending during the application of the specular component to add to the diffuse component and complete the lighting equation.