3.3 Generating Model Normals

Given an arbitrary polygonal model without precomputed normals, it is fairly easy to generate polygon normals for faceted shading, but quite a bit more difficult to create correct vertex normals for smooth shading. A simple cross product of two edges followed by a normalization of the result to obtain a unit-length vector generates a facet normal. Computing a correct vertex normal must take into account all facets that share that normal and whether or not all facets should contribute to the normal. For best results, compute all normals before converting to triangle strips.

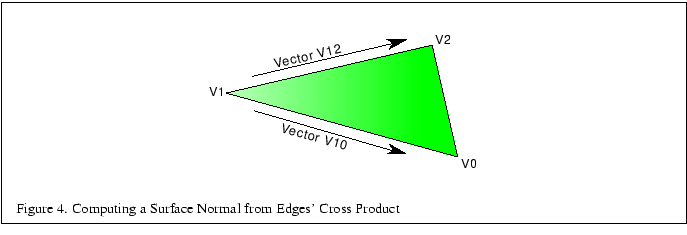
To compute the facet normal of a triangle, select one vertex, compute the vectors from that vertex to the other two vertices, then compute the cross product of those two vectors. Figure 4 shows which vectors to use to compute a cross product for a triangle. The following code fragment generates a facet normal for a triangle, assuming a clockwise polygon winding when viewed from the front:

    /* Compute edge vectors */
    x10 = x1 - x0;
    y10 = y1 - y0;
    z10 = z1 - z0;
    x12 = x1 - x2;
    y12 = y1 - y2;
    z12 = z1 - z2;

    /* Compute the cross product */
    cpx = (z10 * y12) - (y10 * z12);
    cpy = (x10 * z12) - (z10 * x12);
    cpz = (y10 * x12) - (x10 * y12);

    /* Normalize the result to get the unit-length facet normal */
    r = sqrt(cpx * cpx + cpy * cpy + cpz * cpz);
    nx = cpx / r;
    ny = cpy / r;
    nz = cpz / r;

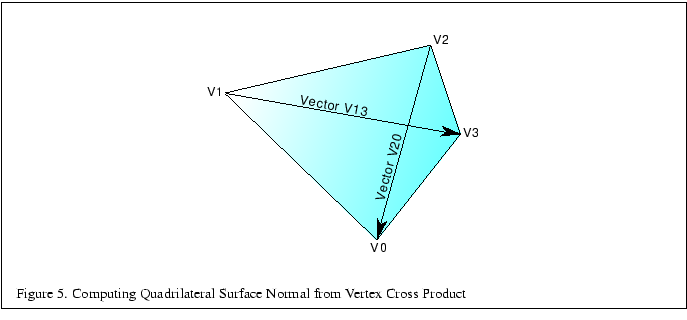
Computing the facet normal of a polygon with more than three vertices is a bit trickier. Often such polygons are not perfectly planar, so you may get a different result depending on which three vertices are chosen. If the polygon is a quadrilateral one good method is to take the cross product of the vectors between opposing vertices as shown in Figure 5. The following code fragment computes the cross product for a quadrilateral:

    /* Compute vectors */
    x20 = x2 - x0;
    y20 = y2 - y0;
    z20 = z2 - z0;
    x13 = x1 - x3;
    y13 = y1 - y3;
    z13 = z1 - z3;

    /* Compute the cross product */
    cpx = (z20 * y13) - (y20 * z13);
    cpy = (x20 * z13) - (z20 * x13);
    cpz = (y20 * x13) - (x20 * y13);

For polygons with more than four vertices it can be difficult to choose the best vertices to use for computing the cross product. It is best to attempt to choose vertices that are the furthest apart from each other, if possible, or average the result of several vertex cross products.