11.2.1.4 Warping a Sphere Map from Cube Views

Yet another approach uses OpenGL's texture mapping capabilities to create the sphere map. Unlike a ray casting approach, the texture warping approach to constructing sphere maps is easily accelerated by graphics hardware. The algorithm renders six cube faces as previously described and copies the results into six respective texture objects using glCopyTexImage2D(). Be sure to align the first cube face view frustum to directly face the viewer. Then the other five cube faces should be aligned with respect to the first. This reliance on the direction to the viewer is because a sphere map is view dependent which will be explained fully later.

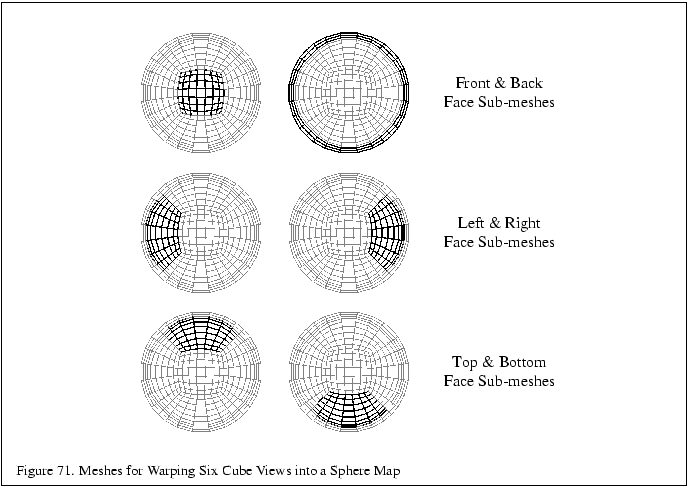
Now, a textured mesh can be drawn to form the actual sphere map. Each one of the six faces becomes a subregion of the mesh. Figure 71 shows the relationship of the submesh for each cube face view to the entire sphere map mesh. The finer the tessellation of the mesh is, the better the warping. In practice, the mesh does not have to be very fine for constructing usable sphere maps.

To render the mesh, first map locations on the cube view faces to unnormalized reflections vectors. Think of each location on a cube view face as a 2D coordinate $(u,v)$ where both $u$ and $v$ range between $[-1,1]$. For example, consider a particular location $(0.3,-0.4)$ on the $Y=-1$ plane face (assuming the front cube view face is oriented on the $Z=+1$ plane so as to face the viewer). This location is mapped to the unnormalized reflection vector $(0.3,-1.0,-0.4)$. Normalize this vector and consider it $\vec{R'}$. Then with this $\vec{R'}$, compute $(s,t)$ using Equations 8 and 9.

Treat $(s,t)$ as a 2D vertex position in the range $[-1,1]$ by $[-1,1]$. Scale by one half and bias by one half the original 2D coordinate, the $(0.3,-0.4)$ coordinate in our example, to map it into the standard $[0,1]$ by $[0,1]$ texture image range. Use this remapped coordinate as a texture coordinate for the 2D vertex position. Setup an orthographic view mapping the $[-1,1]$ by $[-1,1]$ coordinate range into a 128 by 128 pixel region (or whatever resolution sphere map you want to create). Bind to the texture object containing the cube view face rendered image for appropriate face (the $Y=-1$ plane cube view face in our example). Then using the process just described for mapping from a cube face location to a reflection vector to a 2D coordinate, render a mesh of such coordinates, assigning them texture coordinates as described.

The back face mesh must be handled specially. It is not a simple warped rectangular patch, but a mesh in the shape of a ring. Think of the back cube view face as pulled inside-out. In a sphere map, the center of the back cube view face becomes a singularity around the circular edge of the sphere map. The easiest way to render the back face mesh is as four meshes. The construction of these meshes is aided by the reverse mapping equations. Another problem: if a simple polygonal mesh is used, the polygonal edges will not form a perfect sphere. For this reason, it is useful to add a narrow ``extender'' mesh at the circle's edge that makes sure the entire circular sphere map region is rendered. The meshes required are static for a fixed tessellation; compute the meshes once and then re-render for different sets of cube views. Precomputing meshes reduces the overhead for repeated warping of cube face views into sphere map textures.

The final step is to copy the rendered sphere map into a texture using glCopyTexImage2D(). Once this is done, you are ready to use the newly constructed sphere map.