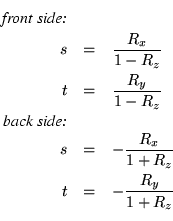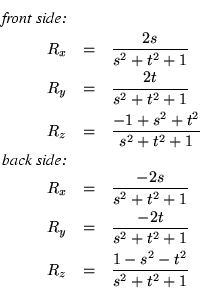


Next: 11.2.2.4 Cheap Per-pixel Lighting
Up: 11.2.2 Dual-Paraboloid Environment Mapping
Previous: 11.2.2.2 Using Dual-Paraboloid Maps
Contents
The main advantages of the dual-paraboloid map approach compared to the sphere
map approach are better sampling of the texture environment, the elimination
of sphere mapping's sparkle artifacts, and view-independence. The last advantage
is important because it allows the viewer, environment mapped object, and the
environment to move with respect to each other without having to continuously regenerate
the dual-paraboloid map. The disadvantage of the dual-paraboloid map
approach are that it requires two rendering passes or the use of multitexturing.
Also constructing the dual-paraboloid map
requires warping two textures instead of just one.
Even though they are view-independent,
dynamic generation of dual-paraboloid maps is still necessary if you want
the environment to be dynamic. The same texture warping approach that is
used to construct sphere maps can be applied to generate dual-paraboloid maps
though the mesh used
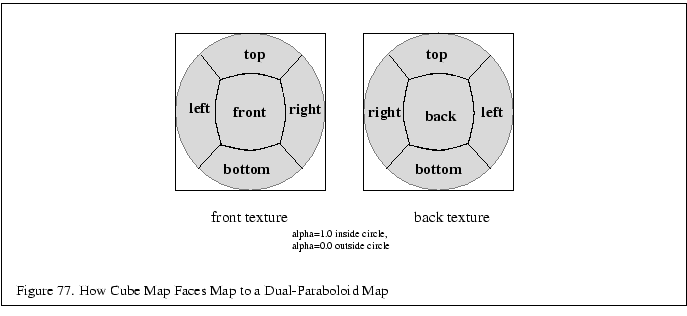
is different. Figure 77 shows how cube map faces are arranged
within the two dual-paraboloid map texture images, and
Figure 78 shows what the texture warping
mesh pattern looks like.
To help in the construction of the texture warping mesh, the
dual-paraboloid mapping
functions for converting
a reflection vector 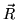 to the front and back 2D texture coordinates
to the front and back 2D texture coordinates 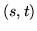 are:
are:
The reverse mapping is:



Next: 11.2.2.4 Cheap Per-pixel Lighting
Up: 11.2.2 Dual-Paraboloid Environment Mapping
Previous: 11.2.2.2 Using Dual-Paraboloid Maps
Contents
2001-01-10


![]() to the front and back 2D texture coordinates
to the front and back 2D texture coordinates ![]() are:
are: