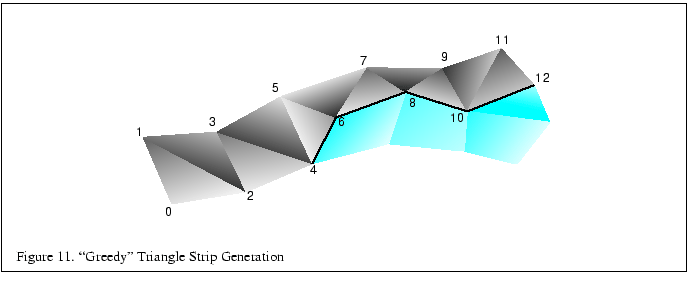
A fairly simple method of converting a model into triangle strips is sometimes known as greedy tri-stripping. One of the early greedy algorithms was developed for IRIS GL that allowed swapping of vertices to create direction changes to the facet with the least neighbors. However, with OpenGL the only way to get the equivalent behavior of swapping vertices is to repeat a vertex and create a degenerate triangle, which is more expensive than the original vertex swap operation.
For OpenGL a better algorithm is to choose a polygon, convert it to triangles, then continue onto the neighboring polygon from the last edge of the previous polygon. For a given starting polygon beginning at a given edge, there are no choices as to which polygon is the best to choose next since there is only one choice. The strip is continued until the triangle strip runs off the edge of the model or runs into a polygon that is already a part of another strip (see Figure 11). For best results, pick a polygon and go both directions as far as possible, then start the triangle strip from one end.

A triangle strip should not cross a hard edge, unless the vertices on that edge are repeated redundantly, since you will want different normals for the two triangles on either side of that edge. Once one strip is complete, the best polygon to choose for the next strip is often a neighbor to the polygon at one end or the other of the previous strip. More advanced triangulation methods do not try to keep all triangles of a polygon together. For more information on such a method refer to [29].