


Next: 13.2.2 Pixel Scale and
Up: 13.2 Colors and Color
Previous: 13.2 Colors and Color
Contents
13.2.1 The Accumulation Buffer: Interpolation and Extrapolation
Haeberli and Voorhies [43] have suggested several interesting
image processing techniques using linear interpolation and extrapolation.
Each technique is stated in terms of the formula:
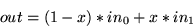 |
(12) |
This equation is evaluated on a per-pixel basis.  and
and  are
the input images,
are
the input images,  is the output image, and
is the output image, and 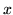 is the blending
factor. If
is the blending
factor. If 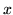 is between
is between 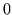 and
and 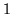 , the equations describe a
linear interpolation. If
, the equations describe a
linear interpolation. If 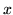 is allowed to range outside
is allowed to range outside ![$[0..1]$](img335.gif) ,
the result is extrapolation [43].
,
the result is extrapolation [43].
In the limited case where
 , these equations may be
implemented using the accumulation buffer via the following steps:
, these equations may be
implemented using the accumulation buffer via the following steps:
- 38.
- Draw
 into the color buffer.
into the color buffer.
- 39.
- Load
 , scaling by
, scaling by  (glAccumGL_ LOAD, (1-x)(GL_ LOAD, (1-x))).
(glAccumGL_ LOAD, (1-x)(GL_ LOAD, (1-x))).
- 40.
- Draw
 into the color buffer.
into the color buffer.
- 41.
- Accumulate
 , scaling by
, scaling by 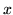 (glAccumGL_ ACCUM,x(GL_ ACCUM,x)).
(glAccumGL_ ACCUM,x(GL_ ACCUM,x)).
- 42.
- Return the results (glAccumGL_ RETURN, 1(GL_ RETURN, 1)).
It is assumed that  and
and  are between
are between 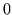 and
and 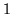 . Since the
accumulation buffer can only store values in the range
. Since the
accumulation buffer can only store values in the range ![$[-1..1]$](img338.gif) , for
the case
, for
the case  or
or  , the equation must be implemented in a
different way. Given the value
, the equation must be implemented in a
different way. Given the value 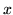 , you can modify equation
12 and derive a list of accumulation buffer
operations to perform the operation. Define a scale factor
, you can modify equation
12 and derive a list of accumulation buffer
operations to perform the operation. Define a scale factor 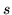 such that:
such that:
Equation 12 becomes:
and the list of steps becomes:
- 43.
- Compute
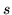 .
.
- 44.
- Draw
 into the color buffer.
into the color buffer.
- 45.
- Load
 , scaling by
, scaling by
 (glAccumGL_ LOAD, (1-x)/s(GL_ LOAD, (1-x)/s)).
(glAccumGL_ LOAD, (1-x)/s(GL_ LOAD, (1-x)/s)).
- 46.
- Draw
 into the color buffer.
into the color buffer.
- 47.
- Accumulate
 , scaling by
, scaling by  (glAccumGL_ ACCUM, x/s(GL_ ACCUM, x/s)).
(glAccumGL_ ACCUM, x/s(GL_ ACCUM, x/s)).
- 48.
- Return the results, scaling by
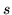 (glAccumGL_ RETURN, s(GL_ RETURN, s)).
(glAccumGL_ RETURN, s(GL_ RETURN, s)).
The techniques suggested by Haeberli and Voorhies use a degenerate
image as  and an appropriate value of
and an appropriate value of 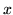 to move toward or away
from that image. To increase brightness,
to move toward or away
from that image. To increase brightness,  is set to a black
image and
is set to a black
image and  . To change contrast,
. To change contrast,  is set to a gray image
of the average luminance value of
is set to a gray image
of the average luminance value of  . Decreasing
. Decreasing 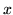 (toward the
gray image) decreases contrast; increasing
(toward the
gray image) decreases contrast; increasing 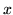 increases contrast. Saturation
may be varied using a luminance version of
increases contrast. Saturation
may be varied using a luminance version of  as
as  . (For
information on converting RGB images to luminance, see
Section 13.2.4.) Sharpening may be accomplished by setting
. (For
information on converting RGB images to luminance, see
Section 13.2.4.) Sharpening may be accomplished by setting
 to a blurred version of
to a blurred version of  [43].
[43].



Next: 13.2.2 Pixel Scale and
Up: 13.2 Colors and Color
Previous: 13.2 Colors and Color
Contents
2001-01-10
![]() , these equations may be
implemented using the accumulation buffer via the following steps:
, these equations may be
implemented using the accumulation buffer via the following steps:
![]() and an appropriate value of
and an appropriate value of ![]() to move toward or away
from that image. To increase brightness,
to move toward or away
from that image. To increase brightness, ![]() is set to a black
image and
is set to a black
image and ![]() . To change contrast,
. To change contrast, ![]() is set to a gray image
of the average luminance value of
is set to a gray image
of the average luminance value of ![]() . Decreasing
. Decreasing ![]() (toward the
gray image) decreases contrast; increasing
(toward the
gray image) decreases contrast; increasing ![]() increases contrast. Saturation
may be varied using a luminance version of
increases contrast. Saturation
may be varied using a luminance version of ![]() as
as ![]() . (For
information on converting RGB images to luminance, see
Section 13.2.4.) Sharpening may be accomplished by setting
. (For
information on converting RGB images to luminance, see
Section 13.2.4.) Sharpening may be accomplished by setting
![]() to a blurred version of
to a blurred version of ![]() [43].
[43].