


Next: 13.2.4.6 CMY Conversion
Up: 13.2.4 The Color Matrix
Previous: 13.2.4.4 Modifying Saturation
Contents
Changing the hue of a color may be accomplished by loading a rotation
about the gray vector 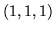 . This operation may be performed in
one step using the glRotate() command. The matrix may also be
constructed via the following steps [42]:
. This operation may be performed in
one step using the glRotate() command. The matrix may also be
constructed via the following steps [42]:
- 49.
- Load the identity matrix (glLoadIdentity()).
- 50.
- Rotate such that the gray vector maps onto the
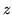 axis using the glRotate() command.
axis using the glRotate() command.
- 51.
- Rotate about the
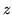 axis to adjust the hue
(glRotate<degrees>, 0, 0, 1(<degrees>, 0, 0, 1)).
axis to adjust the hue
(glRotate<degrees>, 0, 0, 1(<degrees>, 0, 0, 1)).
- 52.
- Rotate the gray vector back into position.
Unfortunately, a naive application of glRotate() will not
preserve the luminance of the image. To avoid this problem, you must
make sure that areas of constant luminance map to planes perpendicular
to the 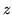 axis when you perform the hue rotation. Recalling that the
luminance of a vector
axis when you perform the hue rotation. Recalling that the
luminance of a vector 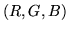 is equal to:
is equal to:
you realize the plane of constant luminance 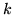 is defined by:
is defined by:
Therefore, the vector
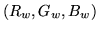 is perpendicular to planes of
constant luminance. The algorithm for matrix construction becomes the
following [42]:
is perpendicular to planes of
constant luminance. The algorithm for matrix construction becomes the
following [42]:
- 53.
- Load the identity matrix.
- 54.
- Apply a rotation matrix
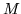 such that the gray vector
such that the gray vector 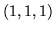 maps onto the positive
maps onto the positive 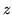 axis.
axis.
- 55.
- Compute
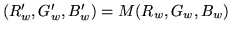 . Apply a skew
transform which maps
. Apply a skew
transform which maps
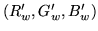 to
to 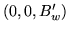 . This
matrix is:
. This
matrix is:
- 56.
- Rotate about the
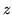 axis to adjust the hue.
axis to adjust the hue.
- 57.
- Apply the inverse of the shear matrix.
- 58.
- Apply the inverse of the rotation matrix.
It is possible to compute a single matrix as a function of 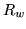 ,
,
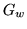 ,
, 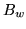 , and the degrees of rotation which performs this
operation.
, and the degrees of rotation which performs this
operation.



Next: 13.2.4.6 CMY Conversion
Up: 13.2.4 The Color Matrix
Previous: 13.2.4.4 Modifying Saturation
Contents
2001-01-10
![]() . This operation may be performed in
one step using the glRotate() command. The matrix may also be
constructed via the following steps [42]:
. This operation may be performed in
one step using the glRotate() command. The matrix may also be
constructed via the following steps [42]:
![\begin{displaymath}
\left[
\begin{array}{c c c c}
1& 0& \frac{-R_w'}{B_w'}& 0 \\...
..._w'}{B_w'}& 0 \\
0& 0& 1& 0 \\
0& 0& 0& 1
\end{array}\right]
\end{displaymath}](img366.gif)