15.1 Non-photorealistic Lighting Models

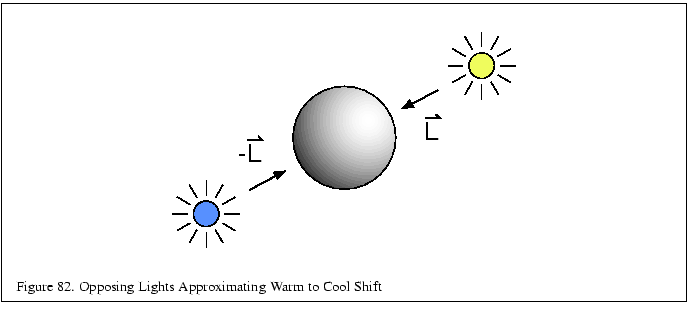
In [39,40] lighting and shading algorithms are developed based on traditional technical illustration practices. A non-photorealistic lighting model for matte and metal surfaces is constructed. The model for matte surfaces use both luminance and hue changes to indicate surface orientation. This lighting model reduces the dynamic range of the luminance, reserving luminance extremes to emphasize edges and highlights. To compensate for the reduced dynamic range and provide additional shape cues, tone-based shading adds hue shifts to the lighting model. Exploiting the relationship that cool colors (blue, violet, green) recede and warm colors (red, orange, yellow) advance, a sense of depth is added by including cool to warm color transitions in the model. The diffuse cosine term is replace with the term:

$$d_{m} ({({{1 + \vec{N} \cdot \vec{L}} \over 2} ) d_{l_{cool}}} + {(1 - {{1 + \vec{N} \cdot \vec{L}} \over 2}) d_{l_{warm}}})$$

where $d_{l_{cool}}$, and $d_{l_{warm}}$ are linear combinations of a cool color (e.g., a shade of blue) combined with the object's diffuse reflectance and a warm color (e.g., yellow) also combined with the object's diffuse reflectance. A typical value for $d_{l_{cool}}$ is $(0., 0., .4) + .2 d_{m}$ and for $d_{l_{warm}}$ is $(.4, .4, 0.) + .6 d_{m}$

This modified diffuse lighting model can be approximated using OpenGL lighting by using two opposed lights ($\vec{L}$, $-\vec{L}$) as shown in Figure 82. The diffuse colors are set to $({d_{l_{warm}} - d_{l_{cool}}})/2$, and $({d_{l_{cool}} - d_{l_{warm}}})/2$, respectively, and the ambient color set to ( ${d_{l_{cool}} + d_{l_{warm}}})/2$ and the specular and emissive contributions set to zero. Objects are drawn with the material reflectances set to one (white). Highlights can be added in a subsequent pass using blending to accumulate the result. Alternatively the environment mapping techniques discussed in Section 10.4 can be used to capture and apply the BRDF at the expensive of computing a map for each different object material.

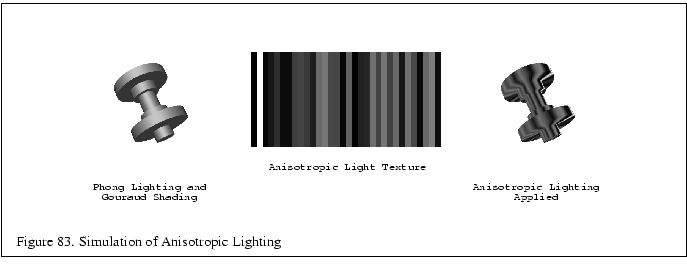
For metallic surfaces, the lighting model is further augmented to simulate the appearance of anisotropic reflection (Section 10.9). While anisotropic reflection typically occurs on machined (milled) metal parts rather than polished parts, the anisotropic model is used to provide a cue that the surfaces are metal and to provide a sense of curvature. To simulate the anisotropic reflection pattern, the curved surface is shaded with stripes along the parametric axis of maximum curvature. The intensity of the stripes are random values between 0.0 and 0.5, except the stripe closest to the light source is set to 1.0 to simulate a highlight. The values between the stripes are interpolated. This process is implemented in the OpenGL pipeline using texture mapping. A small one- or two-dimensional luminance texture is created containing the randomized set of stripe values. The stripe at $s$ coordinate zero (or some well known position) is set to the value one. The object is drawn with texture enabled and the wrap mode set to GL_ CLAMP and the $s$ texture coordinate set to vary along the curvature. The position of the highlight is adjusted by biasing the $s$ coordinate with the texture matrix. This procedure is illustrated in Figure 83.