The ![]() coordinates are transformed in the same fashion as the
coordinates are transformed in the same fashion as the ![]() and
and ![]() coordinates. After transformation, clipping and perspective division,
they occupy the range -1.0 through 1.0. The glDepthRange()
mapping specifies a transformation for the
coordinates. After transformation, clipping and perspective division,
they occupy the range -1.0 through 1.0. The glDepthRange()
mapping specifies a transformation for the ![]() coordinate similar to the
viewport transformation used to map
coordinate similar to the
viewport transformation used to map ![]() and
and ![]() to window coordinates. The
glDepthRange() mapping is somewhat different from the viewport
mapping in that the hardware resolution of the depth buffer is hidden
from the application. The parameters to the glDepthRange() call
are in the range [0.0, 1.0]. The
to window coordinates. The
glDepthRange() mapping is somewhat different from the viewport
mapping in that the hardware resolution of the depth buffer is hidden
from the application. The parameters to the glDepthRange() call
are in the range [0.0, 1.0]. The ![]() or depth associated with a fragment
represents the distance to the eye. By default the fragments nearest
the eye (the ones at the near clip plane) are mapped to 0.0 and the
fragments farthest from the eye (those at the far clip plane) are
mapped to 1.0. Fragments can be mapped to a subset of the depth buffer
range by using smaller values in the glDepthRange() call. The
mapping may be reversed so that fragments furthest from the eye are at
0.0 and fragments closest to the eye are at 1.0 simply by calling
glDepthRange1.0,0.0(1.0,0.0). While this reversal is possible, it may
not be well-suited for some depth buffer implementations. Parts of the underlying
architecture may have been tuned for the forward mapping and may not
produce results of the same quality when the mapping is reversed.
or depth associated with a fragment
represents the distance to the eye. By default the fragments nearest
the eye (the ones at the near clip plane) are mapped to 0.0 and the
fragments farthest from the eye (those at the far clip plane) are
mapped to 1.0. Fragments can be mapped to a subset of the depth buffer
range by using smaller values in the glDepthRange() call. The
mapping may be reversed so that fragments furthest from the eye are at
0.0 and fragments closest to the eye are at 1.0 simply by calling
glDepthRange1.0,0.0(1.0,0.0). While this reversal is possible, it may
not be well-suited for some depth buffer implementations. Parts of the underlying
architecture may have been tuned for the forward mapping and may not
produce results of the same quality when the mapping is reversed.
To understand why there might be this disparity in the rendering
quality, it is important to understand the characteristics of the window
![]() coordinate. The
coordinate. The ![]() value specifies the distance from the fragment to
the plane of the eye. The relationship between distance and
value specifies the distance from the fragment to
the plane of the eye. The relationship between distance and ![]() is linear
in an orthographic projection, but not in a perspective projection. In
the case of a perspective projection, the amount of the non-linearity
is proportional to the ratio of far to near in the glFrustum() call (or
zFar to zNear in the gluPerspective() call).
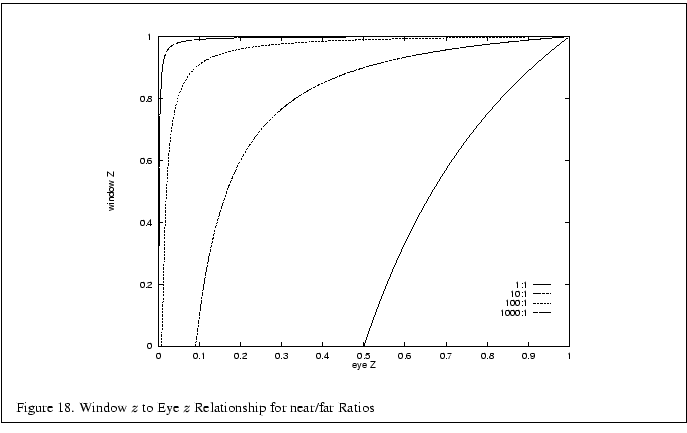
Figure 18 plots the window coordinate
is linear
in an orthographic projection, but not in a perspective projection. In
the case of a perspective projection, the amount of the non-linearity
is proportional to the ratio of far to near in the glFrustum() call (or
zFar to zNear in the gluPerspective() call).
Figure 18 plots the window coordinate ![]() value as a
function of the eye-to-pixel distance for several ratios of far to
near. The non-linearity increases the resolution of the
value as a
function of the eye-to-pixel distance for several ratios of far to
near. The non-linearity increases the resolution of the ![]() -values when
they are close to the near clipping plane, increasing the resolving
power of the depth buffer, but decreasing the precision throughout the
rest of the viewing frustum, thus decreasing the accuracy of the depth
buffer in the back part of the viewing volume.
-values when
they are close to the near clipping plane, increasing the resolving
power of the depth buffer, but decreasing the precision throughout the
rest of the viewing frustum, thus decreasing the accuracy of the depth
buffer in the back part of the viewing volume.
For objects a given distance from the eye, however, the depth
precision is not as bad as it looks in Figure 18.
No matter how far back the far clip plane is, at least half of the
available depth range is present in the first ``unit'' of distance. In
other words, if the distance from the eye to the near clip plane is one
unit, at least half of the ![]() range is used up in the first ``unit''
from the near clip plane towards the far clip plane.
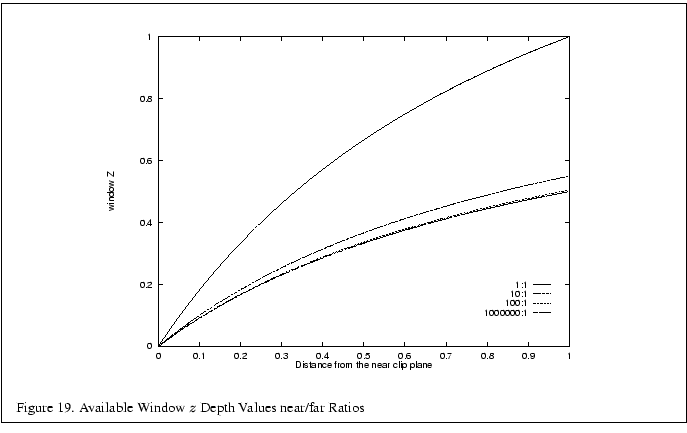
Figure 19 plots the
range is used up in the first ``unit''
from the near clip plane towards the far clip plane.
Figure 19 plots the ![]() range for the first unit
distance for various ranges. With a million to one ratio, the
range for the first unit
distance for various ranges. With a million to one ratio, the ![]() value
is approximately 0.5 at one unit of distance. As long as the data is
mostly drawn close to the near plane, the
value
is approximately 0.5 at one unit of distance. As long as the data is
mostly drawn close to the near plane, the ![]() precision is good. The far
plane could be set to infinity without significantly changing the
accuracy of the depth buffer near the viewer.
precision is good. The far
plane could be set to infinity without significantly changing the
accuracy of the depth buffer near the viewer.
To achieve the best depth buffer precision, the near plane should be
moved as far from the eye as possible without touching the object,
which would cause part or all of it to be clipped away. The position
of the near clipping plane has no effect on the projection of the ![]() and
and
![]() coordinates and therefore has minimal effect on the image.
coordinates and therefore has minimal effect on the image.
Putting the near clip plane closer to the eye than to the object results in loss of depth buffer precision.
In addition to depth buffering, the ![]() coordinate is also used for fog
computations. Some implementations may perform the fog computation on a
per-vertex basis using eye
coordinate is also used for fog
computations. Some implementations may perform the fog computation on a
per-vertex basis using eye ![]() and then interpolate the resulting colors
whereas other implementations may perform the computation for each
fragment. In this case, the implementation may use the window
and then interpolate the resulting colors
whereas other implementations may perform the computation for each
fragment. In this case, the implementation may use the window ![]() to perform
the fog computation. Implementations may also choose to convert the
computation into a cheaper table lookup operation which can also cause
difficulties with the non-linear nature of window
to perform
the fog computation. Implementations may also choose to convert the
computation into a cheaper table lookup operation which can also cause
difficulties with the non-linear nature of window ![]() under perspective
projections. If the implementation uses a linearly indexed table, large far
to near ratios will leave few table entries for the large eye
under perspective
projections. If the implementation uses a linearly indexed table, large far
to near ratios will leave few table entries for the large eye ![]() values.
This can cause noticeable Mach bands in fogged scenes.
values.
This can cause noticeable Mach bands in fogged scenes.