3.1 Modeling Considerations

OpenGL is a renderer not a modeler. There are utility libraries such as the OpenGL Utility Library (GLU) that can assist with modeling tasks, but for all practical purposes modeling is the application's responsibility. Attention to modeling considerations is important; the image quality is directly related to the quality of the modeling. For example, undertessellated geometry produces poor silhouette edges. Other artifacts result from a combination of the model and OpenGL's ordering scheme. For example, interpolation of colors determined as a result of evaluation of a lighting equation at the vertices can result in a less than pleasing specular highlight if the geometry is not sufficiently sampled. We include a short list of modeling considerations with which OpenGL programmers should be familiar:

• Consider using triangles, triangle strips and triangle fans. Primitives such as polygons and quads are usually decomposed by OpenGL into triangles before rasterization. OpenGL does not provide controls over how this decomposition is done, so for more predictable results, the application should do the tessellation directly. Application tessellation is also more efficient if the same model is to be drawn multiple times (e.g., multiple instances per frame, as part of a multipass algorithm, or for multiple frames). The second release of the GLU library (version 1.1) includes a very good general polygon tessellator; it is highly recommended.

• Avoid T-intersections (also called T-vertices). T-intersections occur when one or more triangles share (or attempt to share) a partial edge with another triangle (Figure 1).

   
  

  
  
  

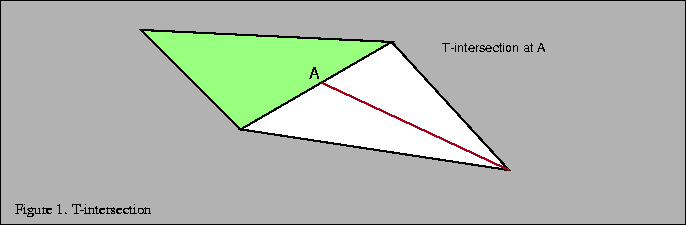
  Even though the geometry may be perfectly aligned when defined, after transformation it is no longer guaranteed to be an exact match. Since finite-precision algorithms are used to rasterize triangles, the edges will not always be perfectly aligned when they are drawn unless both edges share common vertices. This problem typically manifests itself during animations when the model is moved and cracks along the polygon edges appear and disappear. In order to avoid the problem, shared edges should share the same vertex positions so that the edge equations are the same.

  Note that this requirement must be satisfied when seemingly separate models are sharing an edge. For example, an application may have modeled the walls and ceiling of the interior of a room independently, but they do share common edges where they meet. In order to avoid cracking when the room is rendered from different viewpoints, the walls and ceilings should use the same vertex coordinates for any triangles along the shared edges. This often requires adding edges and creating new triangles to ``stitch'' the edges of abutting objects together seamlessly.

• The T-intersection problem has consequences for view-dependent tessellation. Imagine drawing an object in extreme perspective so that some part of the object maps to a large part of the screen and an equally large part of the object (in object coordinates) maps to a small portion of the screen. To minimize the rendering time for this object, applications tessellate the object to varying degrees depending on the area of the screen that it covers. This ensures that time is not wasted drawing many triangles that cover only a few pixels on the screen. This is a difficult mechanism to implement correctly; if the view of the object is changing, the changes in tessellation from frame to frame may result in noticeable motion artifacts. Often it is best to either undertessellate and live with those artifacts or overtessellate and accept reduced performance. The GLU NURBS library is an example of a package that implements view-dependent tessellation and provides substantial control over the sampling method and tolerances for the tessellation.

• Another problem related to T-intersections occurs with careless specification of surface boundaries. If a surface is intended to be closed, it should share the same vertex coordinates where the surface specification starts and ends. A simple example of this would be drawing a sphere by subdividing the interval $[ 0, 2\pi ]$ to generate the vertex coordinates. The vertex at 0 must be the same as the one at $2\pi$. Note that the OpenGL specification is very strict in this regard as even the glMapGrid() routine must evaluate exactly at the boundaries to ensure that evaluated surfaces can be properly stitched together.

• Another consideration is the quality of the attributes that are specified with the vertex coordinates, in particular, the vertex (or face) normals and texture coordinates. When computing normals for an object, sharp edges should have separate normals at common vertices, while smooth edges should have common normals. For example, a cube is made up of six quadrilaterals where each vertex is shared by three polygons, but a different normal should be used for each of the three instances of each vertex, but a sphere is made up of many polygons where all vertices have common normals. Failure to properly set these attributes can result in unnatural lighting effects or shading techniques such as environment mapping will exaggerate the errors resulting in unacceptable artifacts.

• The final suggestion is to be consistent about the orientation of polygons. That is, ensure that all polygons on a surface are oriented in the same direction (clockwise or counterclockwise) when viewed from the outside. The OpenGL face culling method is an efficient form of hidden surface elimination for closed surfaces.