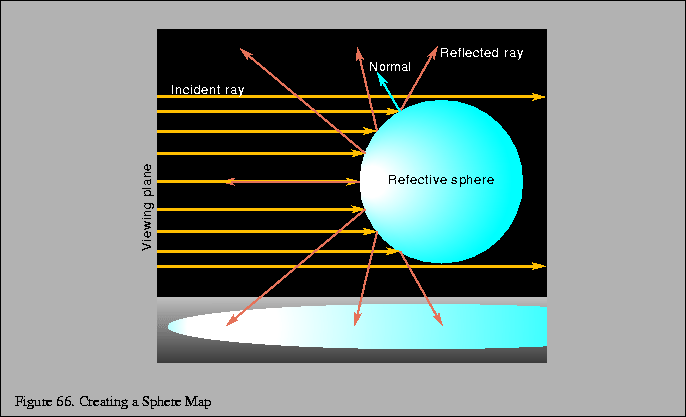

OpenGL has built in support for an environment mapping parameterization know as sphere mapping. Sphere mapping is a type of environment mapping in which the irradiance image is equivalent to that which would be seen in a perfectly reflective hemisphere when viewed using an orthographic projection [76]. This concept is illustrated in Figure 66. The sphere map is computed in the viewing plane. The width and height of the plane are equal to the diameter of the sphere. Rays fired using the orthographic projection are shown in blue (dark gray). In the center of the sphere, the ray reflects back to the viewer. Along the edges of the sphere, the rays are tangent and go behind the sphere.
Note that since the sphere map computes the irradiance at a single point, the sphere is thought of as infinitely small. In effect, you take the limit as the size of the sphere approaches zero. Note that a ray cast at the center of the sphere is bounced directly back at the viewer. Also note that all of the rays along the silhouette edge of the sphere will map to the same point directly behind the sphere in the environment.
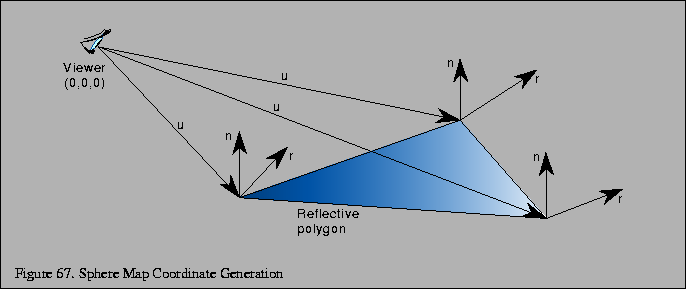
OpenGL provides a texture coordinate generation mode to generate s and t texture coordinates at vertices based on the current normal and the direction to the eye point. The generated coordinates are then used to index a sphere map image which has been bound as a texture.